DBSCAN
(Density-based spatial clustering of applications with noise)
데이터의 밀도를 이용해 군집화하는 알고리즘
'동일한 클래스에 속하는 데이터는 서로 근접하게 분포할 것이다'라는 가정으로 시작
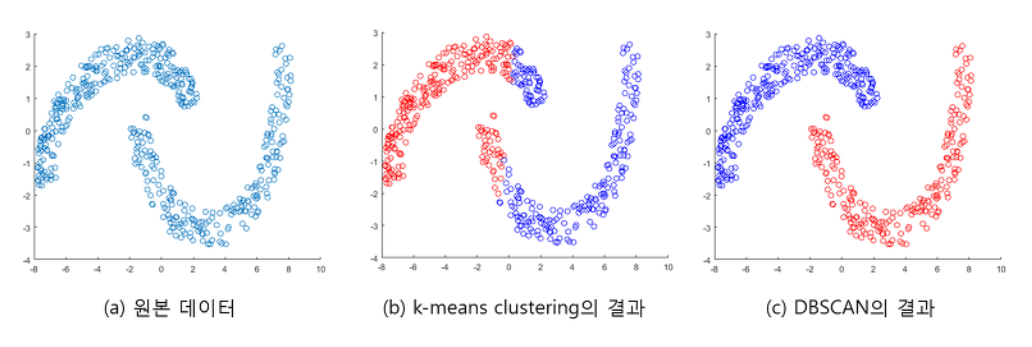
밀도 기반이기에 불특정한 분포의 데이터를 군집화하는데 이용할 수 있다.
위 그림처럼 군집의 형태에 구애받지 않으며
밀도 기반으로 알아서 클러스터링 되기에 군집의 갯수를 사용자가 지정할 필요가 없다.
DBSCAN의 장점
1. 군집 수를 미리 정할 필요가 없다.
2. 불특정한 분포, 기하학적 모양의 군집도 잘 찾아낸다.
(비선형적 클러스터링 가능)
3. 노이즈에 강하다.
(클러스터링 수행 동시에 아웃라이어 분류 가능)
DBSCAN의 단점
1. 데이터 입력 순서에 따라 군집화 결과가 달라질 수 있다.
2. 고차원이거나 데이터의 분포를 모를 경우 적절한 E를 찾기 어렵다.
DBSCAN 동작
Step 1. 임의의 데이터 포인트를 선택
Step 2. 해당 데이터 포인트를 기준으로
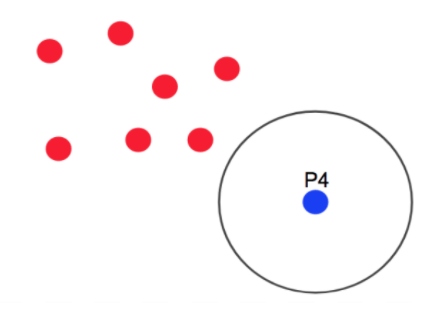
epsilon 만큼의 반경 내에 minPth 개수 이상의 데이터가 있다면 Core point로 할당

최소 데이터 개수를 4로 정한다면 파란점 P가 바로 헥심 벡터가 된다.
헥심 벡터 : 한 데이터 벡터로 부터 거리 E 내에 이웃 데이터가 N개 이상 이상인 데이터
Step 3. 해당 데이터 포인트를 기준으로 epsilon 만큼의 반경 내에
minPth 개수 이상의 데이터가 없다면 Border point로 할당

P1 옆에 있는 P2를 보면
이웃데이터가 스스로를 포함해 총 3개 뿐이기 때문에 핵심 벡터는 되지 못하는 외곽 벡터로 정의된다.
외곽 벡터 : 헥심 벡터가 못되고 해당 클러스터의 외곽을 형성하는 벡터
Step 4. 어떤 데이터 포인트가 Step 2의 조건을 만족하고,
다른 군집에 할당되어있다면 두개의 군집은 연결된것으로 간주하여 하나의 군집으로 할당

P3 또한 핵심 벡터인데 P군집과 겹치기 때문에 하나의 군집으로 클러스터링 된다.
Step 5. 모두 할당 될 때까지 반복
Another Step. 아웃라이어 찾기
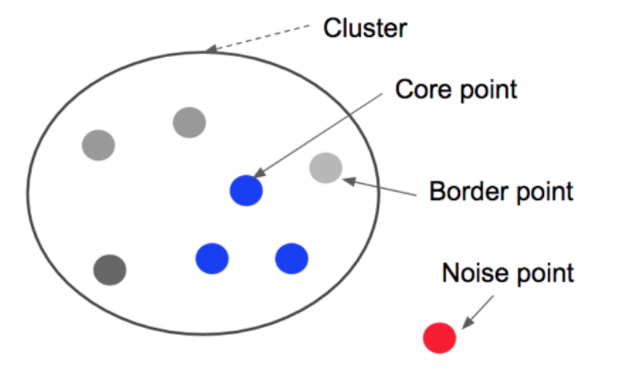
Core point도 Border point에도 해당하지 않아서 군집이 되지 않는 point는
Noise point가 된다.
실전 적용
https://steadiness-193.tistory.com/278
Clustering - K-means
Cluster (클러스터) 비슷한 특성을 가진 데이터들끼리의 묶음 Clustering (클러스터링) 데이터들을 군집(클러스터, 무리)으로 묶어주는 작업 라벨링된 데이터를 묶는 작업으로, 비지도 학습으로 분류�
steadiness-193.tistory.com
위 포스팅에서 전처리 완료한 wine 데이터셋을 이용한다.

DBSCAN 파라미터
eps : 반경의 거리 설정 (실수)
min_samples : core point로 할당하기 위한 최소 근처 데이터 개수 (정수)
metric : 거리를 계산할 때 사용할 메트릭 (Manhattan 또는 Euclidean)
n_jobs : 병렬처리에 사용할 CPU 수
결과 시각화

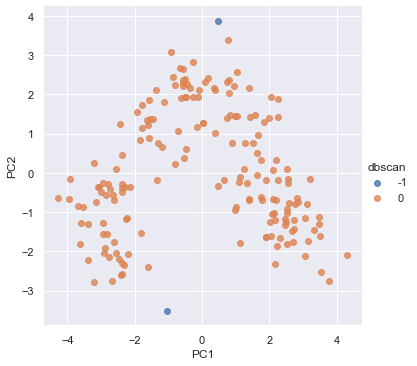
밀도 기반 군집화이고 eps를 1로 설정했으므로 2개의 아웃라이어를 제외하고
모든 포인트가 다 하나의 클러스터로 군집화 되었다.
Core, Border, Noise Point 찾기
DBSCAN 속성
labels_: 군집 번호. -1은 아웃라이어를 의미 (fit_predict한 것과 같은 결과)
core_sample_indices_: 핵심 데이터의 인덱스
아웃라이어, 핵심 데이터에 모두 포함되지 않는다면 경계데이터
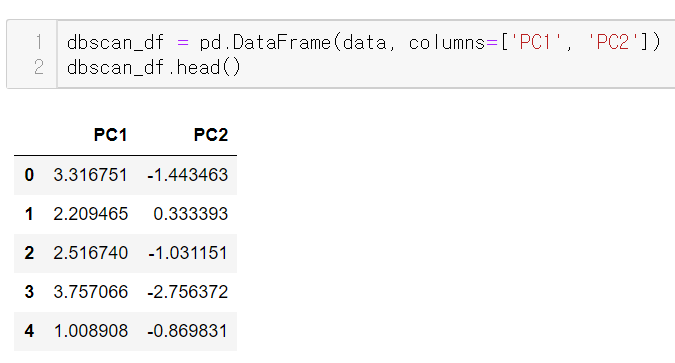
우선 데이터프레임을 만들어 둔다.
아웃라이어 인덱스 찾기
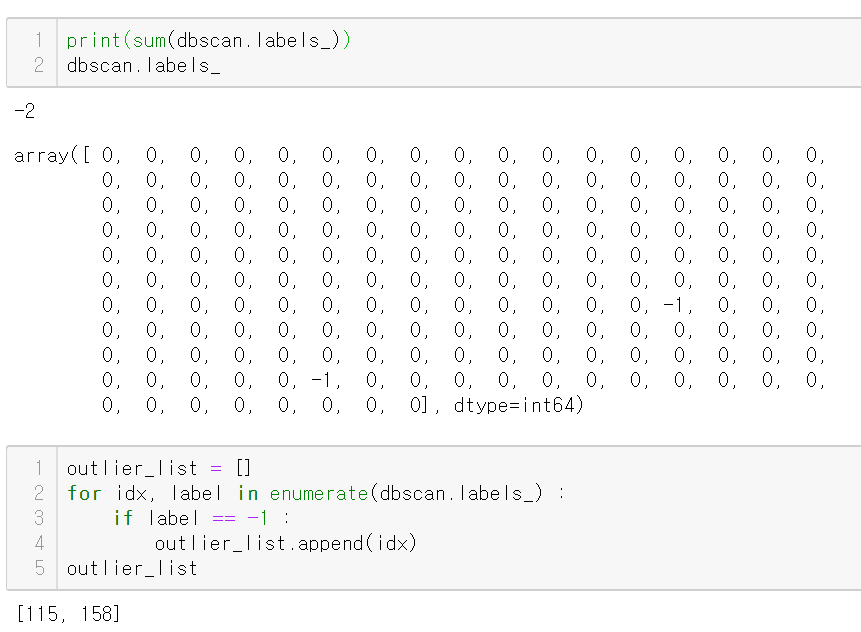
115, 118은 아웃라이어
핵심 포인트 인덱스 찾기

인덱스를 찾아두고 리스트로 바꿔두자
cluster 컬럼 생성

cluster 컬럼에 core, border, outlier를 각각 할당해서 고유값의 개수를 세보았다.
K-means / Hierarchical Clustering / DBSCAN 비교
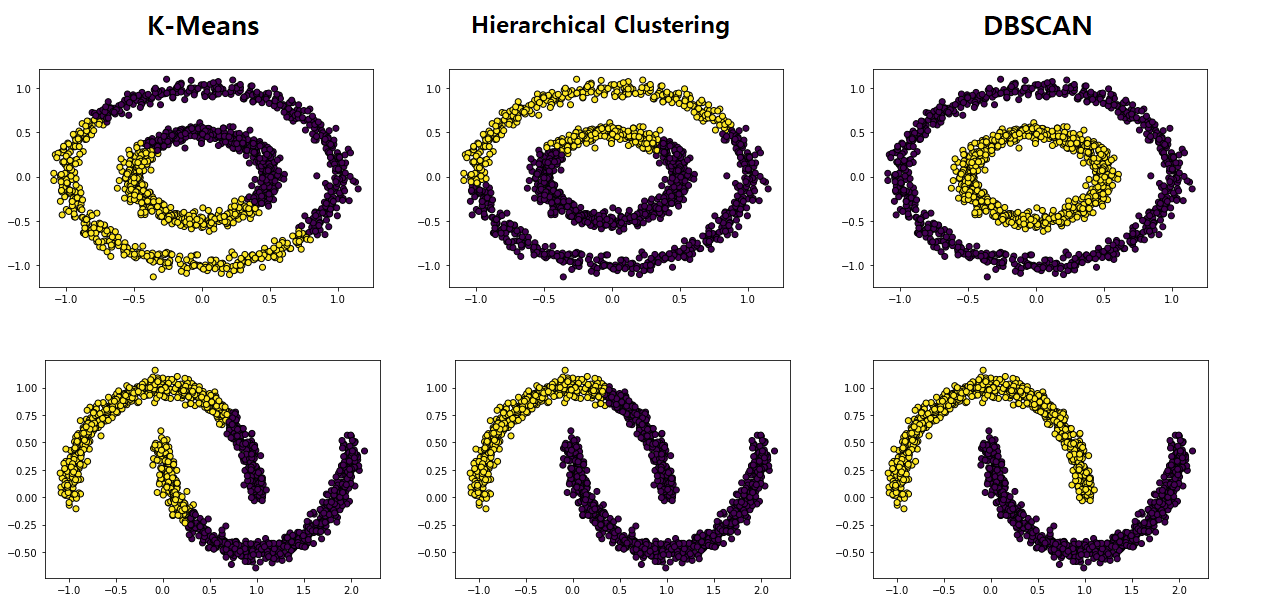
참조
bcho.tistory.com/1205
muzukphysics.tistory.com/147
untitledtblog.tistory.com/146
datascienceschool.net/view-notebook/e335aec955e844a981b41e4e11f79174/
'Machine Learning > 군집(Clustering)' 카테고리의 다른 글
| Clustering - 최적의 군집 수 구하기 : Elbow Method, silhouette, 손실함수 (0) | 2020.09.17 |
|---|---|
| Clustering - 모델 평가 : Silhouette (0) | 2020.09.17 |
| Clustering - Hierarchical Clustering (0) | 2020.09.15 |
| Clustering - K-means (0) | 2020.09.15 |